선형 회귀 분석에서 신뢰 구간(Confidence Interval)과 예측 구간(Prediction Interval)

작성 및 수정 기록

2022년 08월 25일 - 작성 및 공개

 

목차

들어가며

1. 신뢰구간(Confidence Interval)과 예측구간(Prediction Interval)의 의미

2. 신뢰 구간과 예측 구간의 수학적 표현

    1) 신뢰 구간

    2) 예측 구간

    3) 정리

    4) 그래도 부족한 부분

3. 신뢰 구간과 예측 구간 그리기

    1) 수식 활용하기

    2) 함수 활용하기

4. 참고 문헌

 

들어가며

    파이썬으로 배우는 통계학 교과서로 통계 스터디를 하고 있었습니다. 같이 공부하시는 분 중에 항상 허를 찌르는 질문을 해주시는 분이 계신데 아래의 그래프를 보시고 "왜 신뢰구간에 대한 그래프는 곡선이에요?"라고 질문을 하셨습니다. 문제가 생겼습니다. 저도 그 이유를 모른다는 거였습니다. 그래서 한번 열심히 공부해서 왜 곡선인지 설명드려보기로 했습니다. 아래의 그림은 파이썬으로 배우는 통계학 교과서 5장에 나오는 온도에 따른 맥주 매상에 대한 Ordinary Least Square 그래프와 신뢰구간입니다. 

 

 

신뢰구간에 대한 공부를 시작했는데 또 다른 문제가 생겼습니다. 예측 구간은 또 무엇인가요? 설명해야 할 것이 하나 더 늘어서 신뢰 구간(Confidence Interval)과 예측 구간(Prediction Interval) 둘 다에 대해서 정리가 필요하게 되었습니다. 아래는 신뢰 구간, 예측 구간에 대한 예시 그래프입니다.

 

*본 글에서 사용되는 내용 및 데이터는 파이썬으로 배우는 통계학 교과서 5장의 데이터 5-1-1-beer.csv^[1]를 활용하여 작성되었습니다. 다음에 다루긴 할거 같은데 파이썬 통계학 입문으로 참 좋은 책입니다.

 

1. 신뢰구간(Confidence Interval)과 예측구간(Prediction Interval)의 의미

    긴 글을 다 읽기에는 귀찮으신 분들이 있으실 거 같아서 먼저 각각의 의미를 요약해보겠습니다. 

 

1) 신뢰 구간(confidence interval): 모델의 파라미터 변동에 따라서 변하는 수식의 불확실성을 고려한 구간

2) 예측 구간(prediction interval): 모델이 예측하는 y값에 대한 불확실성을 반영하는 구간

    

요약한 글의 단점이기도 하지만 그 문장들만 읽고서는 이해가 안 되는 부분이 생깁니다. 혹시 시간이 괜찮으시다면 저의 시행착오를 따라서 글을 읽어보시면 조금은 이해가 가실 겁니다.

 

2. 신뢰 구간과 예측 구간의 수학적 표현^[4]

    Cosma Rohilla Shalizi의 The Truth about Linear Regression을 보면 선형 회귀에서 신뢰 구간과 예측 구간을 이해하는데 필요한 식이 나옵니다. 자세한 유도는 생략하고 필요한 식들만 설명드리겠습니다. 회귀를 통해서 구해진 식으로부터 표현되는 true conditional mean이 식 1과 같습니다. 

$m(x)\equiv \mathbb{E}[Y|X=x]={\beta }_0+{\beta }_{1}x$

식 1

여기서, ${\beta }_0$와 ${\beta }_1$는 식의 계수입니다. 갑자기 조건부 평균이라니 무슨 말일까요? 우리가 알고 싶은 $x$에 대응하는 $Y$값은 데이터를 통해서 추정되었기 때문에 불확실성을 가지고 있습니다. 불확실성은 일정한 형태의 분포로 표현되며 평균값이 $m(x)$라는 의미가 됩니다. 하나의 예를 들어보겠습니다. 온도가 ${35}^{o}C$일 때 맥주의 매상이 50만 원이라고 예측된다면 항상 50만 원일 까요? 현실세계에서는 그렇지 않을 것입니다. 어떤 날은 30만 원일 때도 있고 어떤 날은 60만 원일 때도 있을 것입니다. 그렇기 때문에 우리가 맥주 매상은 평균값을 가지는 일종의 분포가 될 것입니다.

 

1) 신뢰 구간

    앞에서 했던 이야기를 이어가 보겠습니다. 식 1은 참(true)이었다면 식 2는 조건부 평균의 추정값(estimation of conditional mean)입니다. 데이터에 기반하여서 값을 추정하기 때문에 어느 정도의 불확실성을 가지게 되며 이 불확실성이 식 2에 반영된 것입니다. 

$\hat{m}(x)=\widehat{{\beta }_0}+\widehat{{\beta }_1}x+\frac{1}{n}\sum _{i=1}^n(1+(x-\overline{x})\frac{x_i-\overline{x}}{s_X^2}){ϵ}_i$

식 2

식에서 ^은 추정에 대한 값들을 의미합니다. n은 데이터의 수이며, $\overline{x}$는 $x$의 평균 입니다. ${ϵ}_i$은 여기서 가우시간 노이즈 입니다. $s_X^2$은 아래와 같이 정의됩니다.

$s_X^2=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}{)}^2$

식 3

이제 식을 정리하여 확률 분포를 표현하는 형태로 변경해 보겠습니다.

$\hat{m}(x)\sim N(m(x),\frac{{\sigma }^2}{n}(1+\frac{(x-\overline{x}{)}^2}{s_X^2}))$

식 4

식에서 $\sigma$는 모집단의 표준편차입니다. 식 4는 우리가 추정하려는 $x$에서의 $y$값은 평균이 $m(x)$이고, 분산이 $\frac{{\sigma }^2}{n}(1+\frac{(x-\overline{x}{)}^2}{s_X^2}))$인 확률 분포를 따른다는 의미를 가집니다. 이때 재밌는 점은 분산이 $x$에 대한 2차 방정식의 형태이기 때문에 $x$ 값이 평균 값인 $\overline{x}$에 가까울수록 분산이 작아지게 된다는 것입니다. 이 부분과 관련해서는 후술 하겠습니다.정리해보겠습니다. 선형 회귀를 통해서 도출된 수식은 여러 개의 후보군 중 1개입니다. 그리고 여기에 표현되는 신뢰구간은 우리가 만든 수식의 계수들의 불확실성에 대한 표현입니다. 

 

2) 예측 구간

    예측 구간을 설명할 때 필요한 수식은 신뢰 구간에 사용한 수식과 유사합니다. 확률 변수 $X$가 $x$일 때 $Y$는 평균이 $m(x)$이고 분산이 ${\sigma }^2$입니다. 

$Y|X=x\sim N(m(x),{\sigma }^2)$	식 5
$N(m(x),{\sigma }^2)=\hat{m}(x)+N(0,{\sigma }^2(1+\frac{1}{n}+\frac{(x-\overline{x}{)}^2}{n{s}_X^2})$

선형 회귀를 통해서 도출된 수식을 활용하여 점 $x$에서의 Y값들을 예측한다면 이때 가능한 값들의 집합이 됩니다. 

 

3) 정리

    개념이 유사한 듯 보여서 정리를 한번 해보겠습니다. 신뢰 구간을 설명하는 수식에서는 조건부 평균의 추정(선형 회귀선)을 진행하였고, 예측 구간을 설명하는 수식에서는 확률 변수 $X$가 $x$일 때 $Y$값의 분포에 대해서 설명하였습니다. 

 

4) 그래도 부족한 부분

    하지만 여전히 부족한 부분들이 있습니다. 수식의 설명이 정확하게 맞아떨어지지 않고, 앞서 말한 바와 같이 설명에 필요한 수식이지 신뢰 구간, 예측 구간을 직접 계산하는 수식들이 아닙니다. 그렇다 보니 위의 수식과 인터넷상의 수식을 이용하여서 신뢰 구간과 예측 구간을 그렸을 때 파이썬 라이브러리의 함수가 출력하는 그래프와는 차이를 보입니다. 이점은 추후 공부하면서 수정하도록 하겠습니다.

 

3. 신뢰 구간과 예측 구간 그리기

    먼저, 필요한 라이브러리들을 불러옵니다.

 

import numpy as np
import pandas as pd
import scipy as sp
import scipy.stats as stats
 
import matplotlib.pyplot as plt
import seaborn as sns
 
import statsmodels.formula.api as smf
import statsmodels.api as sm
 
import warnings
warnings.filterwarnings("ignore")
 
# %matplotlib inline

 

이제 사용할 데이터를 불러옵니다. 그 다음으로는 smf.ols를 이용하여 맥주의 매상과 온도 사이의 수식은 만듭니다. 그리고 생성된 수식의 정보를 출력합니다.

 

beer = pd.read_csv("../data/5-1-1-beer.csv")
lm_model = smf.ols(formula = "beer ~ temperature", data=beer).fit()
print(lm_model.summary())

 

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   beer   R-squared:                       0.504
Model:                            OLS   Adj. R-squared:                  0.486
Method:                 Least Squares   F-statistic:                     28.45
Date:                Thu, 25 Aug 2022   Prob (F-statistic):           1.11e-05
Time:                        12:55:19   Log-Likelihood:                -102.45
No. Observations:                  30   AIC:                             208.9
Df Residuals:                      28   BIC:                             211.7
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
===============================================================================
                  coef    std err          t      P>|t|      [0.025      0.975]
-------------------------------------------------------------------------------
Intercept      34.6102      3.235     10.699      0.000      27.984      41.237
temperature     0.7654      0.144      5.334      0.000       0.471       1.059
==============================================================================
Omnibus:                        0.587   Durbin-Watson:                   1.960
Prob(Omnibus):                  0.746   Jarque-Bera (JB):                0.290
Skew:                          -0.240   Prob(JB):                        0.865
Kurtosis:                       2.951   Cond. No.                         52.5
==============================================================================
 
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

 

정보를 확인하였으면 생성된 수식과 신뢰 구간을 그래프를 통해서 확인 합니다.

 

sns.lmplot(x="temperature", y="beer", data=beer)
plt.show()

 

1) 수식 활용하기^[5]

    여기서부터는 앞서 언급했던 수식들을 활용하여서 신뢰 구간과 예측 구간을 그려보겠습니다. 식 4와 식 5의 수식을 이용해서 신뢰 구간과 예측 구간을 구할 수 있는 값들을 계산해 줍니다. 

 

x = beer['temperature']
y_err_ci = x.std() * np.sqrt(1 / len(x) + (x - x.mean()) ** 2 / np.sum((x - x.mean()) ** 2))
y_err_pi = x.std() * np.sqrt(1 + 1 / len(x) + (x - x.mean()) ** 2 / len(x) / np.sum((x - x.mean()) ** 2))

 

다음으로는 값들을 모아서 하나의 DataFame으로 만들어 줍니다.

 

data = {'temperature': beer['temperature'],
        'beer': beer['beer'],
        'lm_predict': lm_predict,
        'y_err_ci': y_err_ci,
        'y_err_pi': y_err_pi}
 
lm_beer = pd.DataFrame(data)
print(lm_beer.head())

 

그리고 결과를 확인합니다. 여기서 한 가지 작업이 필요합니다. 온도의 값이 오름차순으로 되어 있지 않기 때문에 추후에 사용할 plt.fill_between에서 정상적으로 그래프가 출력되지 않습니다.

 

   temperature  beer  lm_predict  y_err_ci   y_err_pi
0         20.5  45.3   50.301481  1.800246  10.022146
1         25.0  59.3   53.745905  1.996425  10.023385
2         10.0  40.4   42.264491  2.633247  10.028286
3         26.9  38.0   55.200217  2.172442  10.024605
4         15.8  37.0   46.703971  1.988464  10.023332

 

Pandas의 sort_values를 이용하여 온도를 기준으로 오름 차순 정렬을 진행합니다.

 

lm_beer = lm_beer.sort_values('temperature')
print(lm_beer.head())

 

값이 정상적으로 정렬된 것을 확인할 수 있습니다.

 

    temperature  beer  lm_predict  y_err_ci   y_err_pi
5           4.2  40.9   37.825011  3.497712  10.037090
29          6.4  38.8   39.508952  3.154448  10.033298
23          7.9  38.2   40.657093  2.930021  10.031029
14          8.4  37.4   41.039807  2.857330  10.030330
9           8.5  44.9   41.116350  2.842932  10.030194

 

전체 그래프로 넘어가기 전에 신뢰 구간과 예측 구간에 대한 그래프의 형태를 보고 가겠습니다. 신뢰 구간에 대한 식은 $x$에 대한 2차였기 때문에 곡선의 형태를 가집니다.  예측 구간 역시 2차 식 형태였지만 수식의 차이로 인해서 크게 변화가 없는 형태의 그래프가 됩니다.

 

plt.figure(figsize=(6, 6))
 
yrange = [1, 12]
x_mean = lm_beer['temperature'].mean()
plt.plot([x_mean, x_mean], yrange,
         linestyle='dashed', color='red', alpha=0.5, label='x mean')
 
plt.plot(lm_beer['temperature'], lm_beer['y_err_pi'], label='Predcition interval')
plt.plot(lm_beer['temperature'], lm_beer['y_err_ci'], label='Confidence interval')
 
plt.xlabel('temperature')
plt.ylim(yrange)
plt.legend()
plt.show()

 

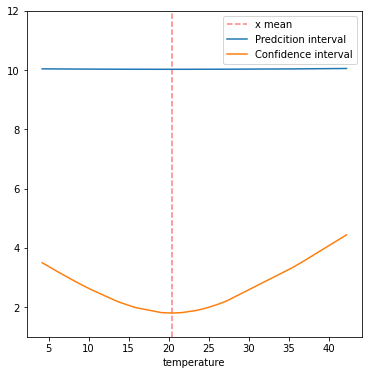
이번에는 신뢰 구간과 예측 구간에 대한 값들은 선형 회귀 식에서 더하고 빼서 그래프를 그려보겠습니다. 우리가 원하는 모양의 그래프가 만들어졌습니다. 위의 그래프처럼 명확하지는 않지만 $\overline{x}$ 부근에서 오목한 형태가 됩니다.

 

plt.figure(figsize=(6, 6))
 
yrange = [25, 80]
x_mean = lm_beer['temperature'].mean()
plt.plot([x_mean, x_mean], yrange,
         linestyle='dashed', color='red', alpha=0.5, label='x mean')
 
plt.fill_between(lm_beer['temperature'], 
                 lm_beer['lm_predict'] - lm_beer['y_err_pi'], 
                 lm_beer['lm_predict'] + lm_beer['y_err_pi'], 
                 alpha=0.1, label='Prediction interval')
 
plt.fill_between(lm_beer['temperature'], 
                 lm_beer['lm_predict'] - lm_beer['y_err_ci'], 
                 lm_beer['lm_predict'] + lm_beer['y_err_ci'], 
                 alpha=0.3, label='Confidence interval')
 
plt.scatter(lm_beer['temperature'], lm_beer['beer'], 
            marker='o', color='black', label='Observed')
 
plt.plot(lm_beer['temperature'], lm_beer['lm_predict'], 
         color='blue', label='Regression line')
 
plt.xlabel('temperature')
plt.ylabel('beer')
plt.ylim(yrange)
plt.legend()
plt.show()

 

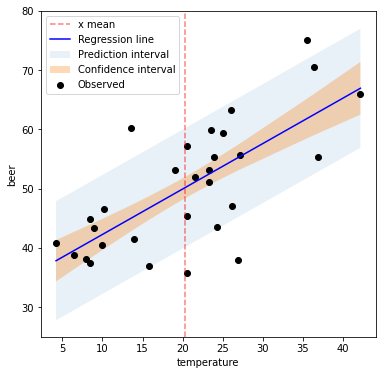
다음으로는 수식으로 그린 신뢰 구간과 함수에서 보여주는 신뢰 구간을 비교해 보겠습니다. 형태는 대략적으로 비슷하지만 차이가 있는 것을 확인할 수 있습니다. 이는 아마도 2. 신뢰 구간과 예측 구간의 수학적 표현 - 4) 그래도 부족한 부분에서 언급한 문제들 때문일 것입니다.

 

sns.lmplot(x="temperature", y="beer", data=beer)
 
plt.fill_between(lm_beer['temperature'], 
                 lm_beer['lm_predict'] - lm_beer['y_err_ci'], 
                 lm_beer['lm_predict'] + lm_beer['y_err_ci'], 
                 alpha=0.5)
 
plt.legend(labels=['Regression line', 'Observed', 'CI lmplot', 'CI Equation'])
plt.show()

 

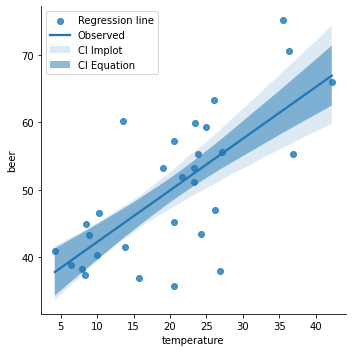
2) 함수 활용하기^[6]

    수식을 활용한 방법 이외에 함수를 활용하여서 신뢰 구간과 예측 구간을 그려보겠습니다. 이때는 앞서 생성한 lm_model에 get_prediction과 summary_frame을 사용합니다. summary_frame은 설명 문서가 없이 소스 코드로 연결됩니다. 생성된 결과를 확인해봅니다. 마찬가지로 온도를 기준으로 오름 차순 정렬을 진행합니다.

 

predictions = lm_model.get_prediction(beer['temperature']).summary_frame()
predictions = predictions.sort_values('temperature')
print(predictions.head())

 

데이터 중 mean_ci로 시작하는 데이터들이 신뢰 구간에 해당하고 obs_ci로 시작하는 데이터들이 예측 구간에 해당합니다.

 

         mean   mean_se  mean_ci_lower  mean_ci_upper  obs_ci_lower  \
5   37.825011  2.703143      32.287874      43.362149     21.264113   
29  39.508952  2.437858      34.515227      44.502677     23.121739   
23  40.657093  2.264413      36.018652      45.295534     24.374630   
14  41.039807  2.208235      36.516442      45.563172     24.789752   
9   41.116350  2.197109      36.615777      45.616923     24.872624   
 
    obs_ci_upper  temperature  
5      54.385910          4.2  
29     55.896165          6.4  
23     56.939556          7.9  
14     57.289862          8.4  
9      57.360075          8.5

 

상한 값들과 하한 값들을 활용하여 그래프를 그리면 아래와 같이 데이터, 선형 회귀선, 신뢰 구간 그리고 예측 구간을 그릴 수 있습니다.

 

plt.figure(figsize=(6, 6))
plt.fill_between(predictions['temperature'], predictions['obs_ci_lower'], predictions['obs_ci_upper'], 
                 alpha=.1, label='Prediction interval')
plt.fill_between(predictions['temperature'], predictions['mean_ci_lower'], predictions['mean_ci_upper'], 
                 alpha=.5, label='Confidence interval')
plt.scatter(beer['temperature'], beer['beer'], marker='o', color='black', label='Observed')
plt.plot(predictions['temperature'], predictions['mean'], color='blue', label='Regression line')
 
plt.xlabel('temperature')
plt.ylabel('beer')
plt.legend()
plt.show()

 

참고 문헌

[1] 파이썬으로 배우는 통계학 교과서; 바바 신야 지음, 윤옹식 옮김; 한빛미디어 (2020)

[2] https://stats.stackexchange.com/questions/85560/shape-of-confidence-interval-for-predicted-values-in-linear-regression
[3] https://people.duke.edu/~rnau/mathreg.htm

[4] The Truth about Linear Regression; Cosma Rohilla Shalizi; 2019; Chapter 8 - Predictive Inference for the Simple Linear Model 

[5] https://matplotlib.org/3.1.3/gallery/lines_bars_and_markers/fill_between_demo.html#sphx-glr-gallery-lines-bars-and-markers-fill-between-demo-py

[6] https://lmc2179.github.io/posts/confidence_prediction.html

 

긴 글 읽어주셔서 감사합니다. 
글과 관련된 의견은 언제든지 환영입니다.